SAT점수와 성별로 입학여부를 로지스틱 회귀분석으로 학습하고 그 결과를 PLOT 하는 소스코드를 작성하였습니다. 그리고 국가별 위도/경도 정보를 군집분석하여 그 결과를 PLOT 하는 소스코드를 작성합니다. 빙 chat GPT에게 위 내용을 질문하여 얻은 결과이며 결과는 실습과 동일합니다.
미국 입학시험 (SAT) 결과 와 성별에 따른 입력여부 로지스틱 회귀분석
분석대상 데이터
| SAT | Admitted | Gender |
| 1363 | No | Male |
| 1792 | Yes | Female |
| 1954 | Yes | Female |
| 1653 | No | Male |
먼저 데이터세트를 질문하여 표로 요약한 결과는 다음과 같습니다.
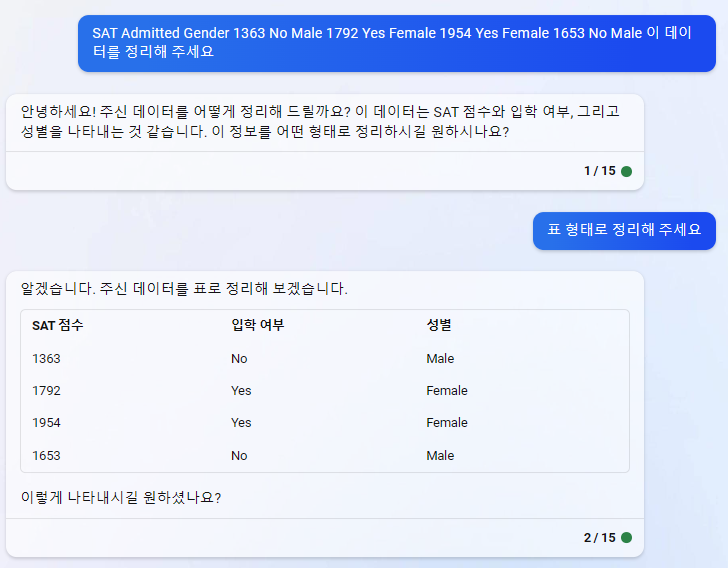
소스코드 생성요청한 질문 결과는 다음과 같으며, 소스코드도 작성합니다.
질문 ) SAT 점수와 성별을 독립변수로하여 입학여부를 로직스틱 회귀분석하는 파이선 3.8 소스코드와 SAT 점수 평균으로 확률을 표현하는 PLOT 코드 생성
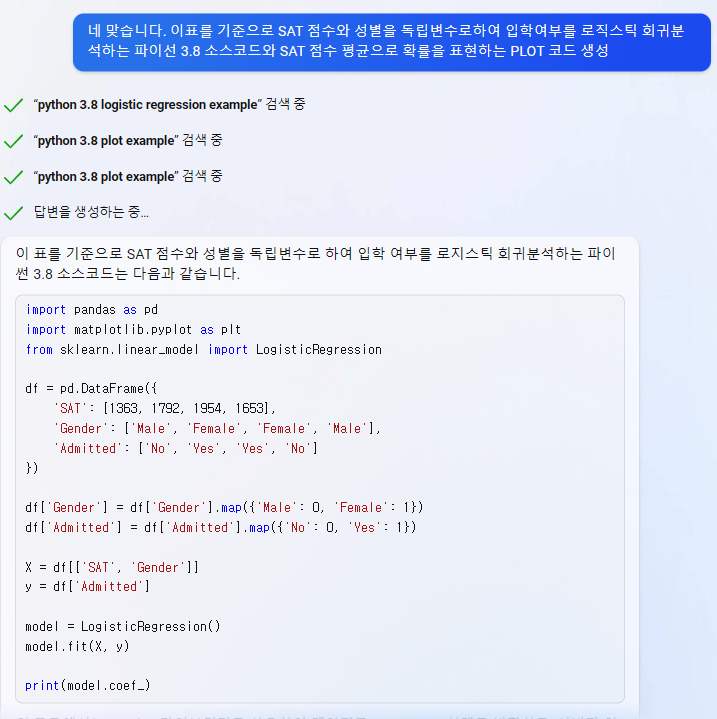
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
df = pd.DataFrame({
'SAT': [1363, 1792, 1954, 1653],
'Gender': ['Male', 'Female', 'Female', 'Male'],
'Admitted': ['No', 'Yes', 'Yes', 'No']
})
df['Gender'] = df['Gender'].map({'Male': 0, 'Female': 1})
df['Admitted'] = df['Admitted'].map({'No': 0, 'Yes': 1})
X = df[['SAT', 'Gender']]
y = df['Admitted']
model = LogisticRegression()
model.fit(X, y)
print(model.coef_)import numpy as np
x = np.linspace(1300, 2000, 100)
y = model.predict_proba(np.column_stack((x, np.ones_like(x))))[:,1]
plt.plot(x,y)
plt.xlabel('SAT')
plt.ylabel('Probability of Admission')
plt.show()import numpy as np
import pandas as pd
from sklearn.linear_model import LogisticRegression
df = pd.DataFrame({
'SAT': [1363, 1792, 1954, 1653],
'Gender': ['Male', 'Female', 'Female', 'Male'],
'Admitted': ['No', 'Yes', 'Yes', 'No']
})
df['Gender'] = df['Gender'].map({'Male': 0, 'Female': 1})
df['Admitted'] = df['Admitted'].map({'No': 0, 'Yes': 1})
X = df[['SAT', 'Gender']]
y = df['Admitted']
model = LogisticRegression()
model.fit(X, y)
print(model.coef_)위 코드에서는 pandas 라이브러리를 사용하여 데이터를 DataFrame 형태로 변환하고, 성별과 입학 여부의 값을 숫자로 변환합니다. 그리고 로지스틱 회귀분석 모델을 생성하고 학습시킨 후, 계수(coefficient)를 출력합니다.
또한 SAT 점수 평균으로 확률을 표현하는 PLOT 코드는 다음과 같습니다.
import numpy as np
x = np.linspace(1300, 2000, 100)
y = model.predict_proba(np.column_stack((x, np.ones_like(x))))[:,1]
plt.plot(x,y)
plt.xlabel('SAT')
plt.ylabel('Probability of Admission')
plt.show()위 코드에서는 numpy와 matplotlib 라이브러리를 사용하여 SAT 점수 범위에 대한 예측값을 계산하고 그래프로 출력합니다. 참고로 위 코드에서는 모든 데이터가 주어졌다는 가정하에 작성된 것입니다. 만약 실제 데이터가 더 많다면 이를 고려하여 모델을 수정해야 할 수도 있습니다.
플로팅 결과
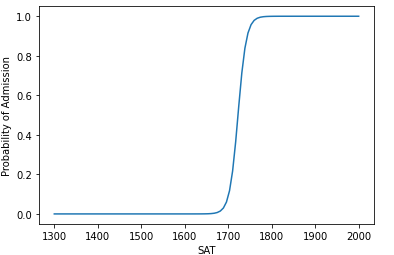
국가별 위도/경도 정보 군집분석
분석대상 데이터
| name | Longitude | Latitude | continent |
| Aruba | -69.98267711 | 12.52088038 | North America |
| Afghanistan | 66.00473366 | 33.83523073 | Asia |
| Angola | 17.53736768 | -12.29336054 | Africa |
| Anguilla | -63.06498927 | 18.2239595 | North America |
| Albania | 20.04983396 | 41.14244989 | Europe |
| Aland | 19.95328768 | 60.21488688 | Europe |
| Andorra | 1.56054378 | 42.54229102 | Europe |
| United Arab Emirates | 54.3001671 | 23.90528188 | Asia |
먼저 데이터세트를 질문하여 표로 요약한 결과는 다음과 같습니다.
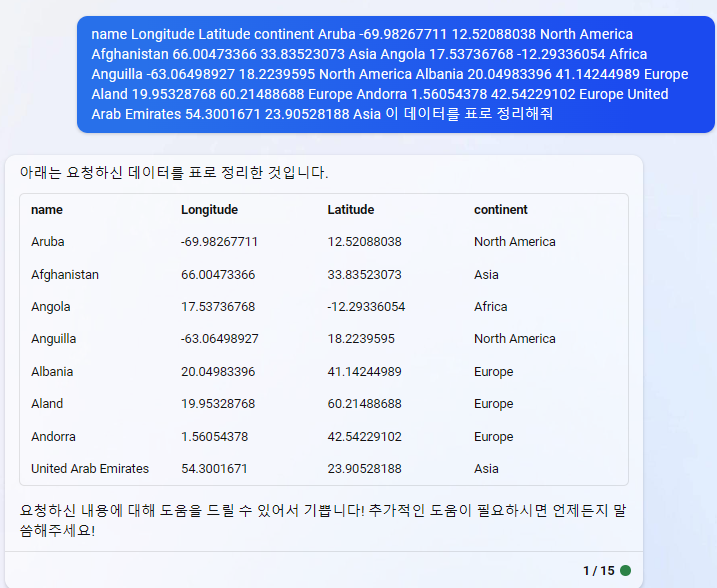
소스코드 생성요청한 질문 결과는 다음과 같으며, 소스코드도 작성합니다.
질문 ) 위 표의 내용을 파이선 3.8 소스코드로 군집분석 최적 k를 산출하는 방법과 최적 k를 기준으로 군집영역을 색상으로 표기하는 PLOT 코드 생성
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
# X is the dataset
country= pd.read_csv('countries.csv')
X = country.iloc[:,1:3]
X = np.array(X)
wcss = []
for i in range(1, 11):
kmeans = KMeans(n_clusters=i, init='k-means++', max_iter=300, n_init=10, random_state=0)
kmeans.fit(X)
wcss.append(kmeans.inertia_)
plt.plot(range(1, 11), wcss)
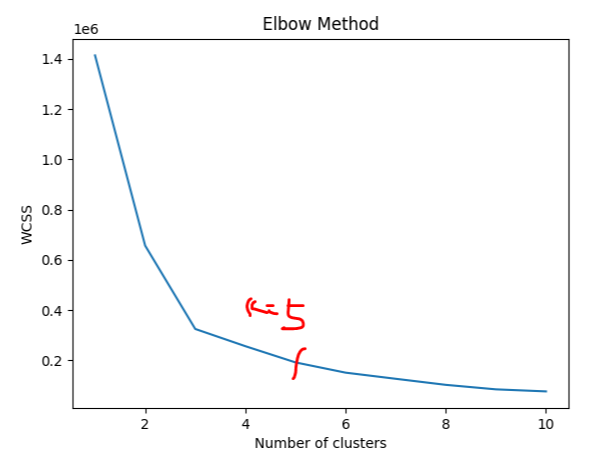
plt.title('Elbow Method')
plt.xlabel('Number of clusters')
plt.ylabel('WCSS')
plt.show()kmeans = KMeans(n_clusters=optimal_k, init='k-means++', max_iter=300, n_init=10, random_state=0)
pred_y = kmeans.fit_predict(X)
plt.scatter(X[:,0], X[:,1])
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s=300, c='red')
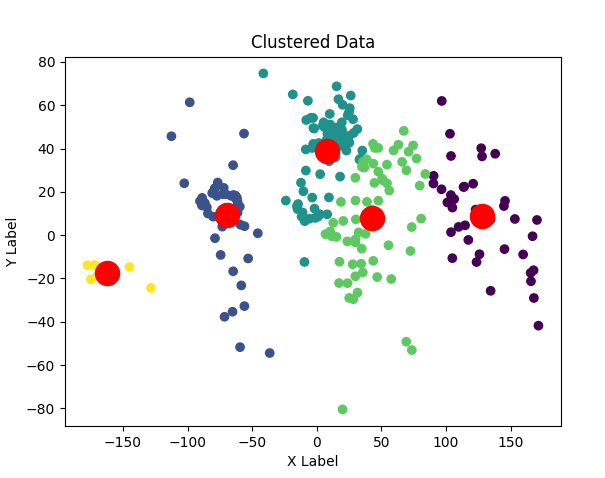
plt.title('Clustered Data')
plt.xlabel('X Label')
plt.ylabel('Y Label')
plt.show()군집분석에서 최적 k를 찾는 방법은 여러가지가 있습니다. 그중 하나는 Elbow Method입니다. 이 방법은 클러스터의 개수(K)를 변화시키면서 클러스터 내부의 분산과 전체 분산의 비율을 계산하여 그래프로 나타내고, 그래프에서 기울기가 급격하게 감소하는 지점이 최적 K라고 판단합니다.
아래는 파이썬 3.8에서 Elbow Method를 사용하여 최적 K를 찾는 코드입니다:
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
# X is the dataset
country= pd.read_csv('countries.csv')
X = country.iloc[:,1:3]
X = np.array(X)
wcss = []
for i in range(1, 11):
kmeans = KMeans(n_clusters=i, init='k-means++', max_iter=300, n_init=10, random_state=0)
kmeans.fit(X)
wcss.append(kmeans.inertia_)
plt.plot(range(1, 11), wcss)
plt.title('Elbow Method')
plt.xlabel('Number of clusters')
plt.ylabel('WCSS')
plt.show()위 코드에서 X는 데이터셋을 나타냅니다. 이 코드를 실행하면 Elbow Method 그래프가 생성되며 최적 K값을 찾을 수 있습니다. 그리고 최적 K값을 기준으로 군집영역을 색상으로 표기하는 PLOT 코드는 다음과 같으며, 최적 k의 변수는 optimal_k입니다.
kmeans = KMeans(n_clusters=optimal_k, init='k-means++', max_iter=300, n_init=10, random_state=0)
pred_y = kmeans.fit_predict(X)
plt.scatter(X[:,0], X[:,1])
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s=300, c='red')
plt.title('Clustered Data')
plt.xlabel('X Label')
plt.ylabel('Y Label')
plt.show()플로팅 결과
'IT > 오랫만코딩:파이썬' 카테고리의 다른 글
| DAY12 특징선택-feature selection 및 재현율 (recall)-(Bing 챗(chat) GPT 생성한 파이썬 코드 첨삭) (1) | 2023.03.21 |
|---|---|
| DAY 09 머신러닝 관련 Bing 챗(chat) GPT 생성한 파이썬 코드 및 동일 절차 Weka 실행 (0) | 2023.03.16 |
| DAY07 통계검정 (with OpenAI/Bing 챗(chat) GPT 생성한 파이썬 코드 첨삭) (0) | 2023.03.14 |
| DAY06 통계정리 (with OpenAI/Bing 챗(chat) GPT 생성한 파이썬 코드 첨삭) (0) | 2023.03.13 |
댓글