저의 아킬레스건인 통계내용을 파이썬을 이용하여 정리해 봅니다. 교육에서 알려준 예시들을 상황에 맞는 분포함수를 사용하여 정리하고 코드를 기록합니다. 코드는 강의에서 내용을 복기하기 위해 OpenAI와 Bing 챗(chat) GPT를 사용하여 작성하였습니다.
균등분포 함수
예제) 어느 주식의 하루 동안 오를 확률과 내릴 확률이 50%라고 하자. 또한 매일 매일의 주가의 움직임은 독립이다. 이 주식의 가격이 1주일 동안 오를 확률은? 균등분포 함수를 사용하는 파이썬 코드
Chat GPT 답변)
주식의 가격이 1주일 동안 오를 확률은 이항분포를 사용하여 계산할 수 있습니다. 이항분포는 베르누이 시행을 n번 반복하여 그중 성공하는 횟수를 X라고 할 때, 이 X가 따르는 분포입니다. 여기서는 1주일 동안 7번의 베르누이 시행을 하게 됩니다.
파이썬에서는 이항분포 확률질량함수를 계산하기 위해 scipy.stats.binom.pmf 함수를 사용할 수 있습니다.
아래는 이 문제를 해결하기 위한 파이썬 코드입니다.
from scipy.stats import binom
# 하루 동안 오를 확률과 내릴 확률이 50%인 경우
p = 0.5
# 1주일 동안 7번의 시행이 있으므로 n = 7
n = 7
# 1주일 동안 오를 확률을 구하기 위해 X = 4인 경우의 확률을 계산
# 이는 7일 중에서 4일 동안 상승하고 3일 동안 하락할 확률을 의미함
prob = binom.pmf(4, n, p)
print("1주일 동안 주식 가격이 오를 확률은 {:.2f}%입니다.".format(prob * 100))

예제) 어느 햄버거 가게에서 고객들의 1인당 지불액을 보니 10,000원부터 15,000원까지 균등하게 분포되어 있다. 어떤 고객이 14,000원 이상을 지불할 확률은?
Chat GPT 답변)
고객들의 1인당 지불액이 10,000원부터 15,000원까지 균등분포를 따른다는 것은 확률밀도함수가 다음과 같다는 것을 의미합니다.
이제 고객이 14,000원 이상을 지불할 확률을 구해보겠습니다. 이는 구간 [14,000, 15,000]에서의 확률값을 구하는 것과 같습니다. 따라서 다음과 같이 코드를 작성할 수 있습니다.
# 구간 시작점
a = 14000
# 구간 끝점
b = 15000
# 확률밀도함수
f = 0.0005
# 14,000원 이상을 지불할 확률 계산
p = (b - a) * f
print("14,000원 이상을 지불할 확률은 {:.2f}%입니다.".format(p * 100))

예제) 로지스틱 분포를 따르는 난수 생성하기 균등분포 파이썬 코드
# 로지스틱 분포를 따르는 난수를 생성하는 파이썬 코드는 다음과 같습니다:
import numpy as np
# 로지스틱 분포의 위치와 모양을 결정하는 매개변수
loc = 0
scale = 1
# 난수의 개수
size = 10
# 로지스틱 분포에서 난수 생성
logistic_random_numbers = np.random.logistic(loc, scale, size)
print(logistic_random_numbers)
#균등분포에서 난수를 생성하는 파이썬 코드는 다음과 같습니다:
import numpy as np
# 균등분포의 하한과 상한
low = 0
high = 1
# 난수의 개수
size = 10
# 균등분포에서 난수 생성
uniform_random_numbers = np.random.uniform(low, high, size)
print(uniform_random_numbers)

이항분포
예제) 한번의 클릭이 판매로 이어질 확률이 0.01일 때, 200회 클릭이 1번 이상의 구매로 이어질 확률은?
from scipy.stats import binom
# 성공 확률
p = 0.01
# 시행 횟수
n = 200
# 구매가 일어난 횟수가 k번 이상일 확률
k = 1
# 누적 분포 함수를 사용하여 k-1번 이하의 구매가 일어날 확률을 계산
prob_less_than_k = binom.cdf(k-1, n, p)
# k번 이상의 구매가 일어날 확률은 1에서 k-1번 이하의 구매가 일어날 확률을 뺀 값
prob_at_least_k = 1 - prob_less_than_k
print(f"200회 클릭 중에서 1번 이상의 구매가 일어날 확률: {prob_at_least_k:.4f}")

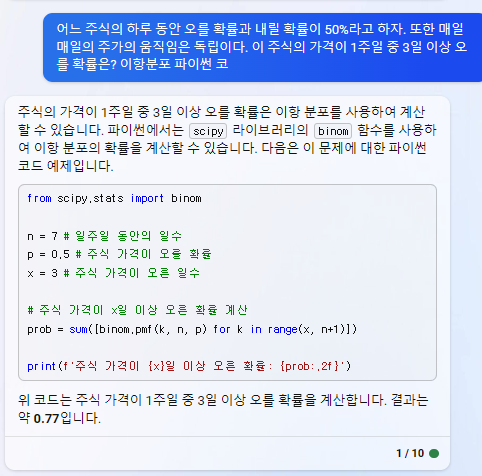
예제) 어느 주식의 하루 동안 오를 확률과 내릴 확률이 50%라고 하자. 또한 매일의 주가의 움직임은 독립이다. 이 주식의 가격이 1주일 중 3일 이상 오를 확률은?
from scipy.stats import binom
n = 7 # 일주일 동안의 일수
p = 0.5 # 주식 가격이 오를 확률
x = 3 # 주식 가격이 오른 일수
# 주식 가격이 x일 이상 오른 확률 계산
prob = sum([binom.pmf(k, n, p) for k in range(x, n+1)])
print(f'주식 가격이 {x}일 이상 오른 확률: {prob:.2f}')
답변) 위 코드는 주식 가격이 1주일 중 3일 이상 오를 확률을 계산합니다. 결과는 약 0.77입니다.
정규분포
예제)
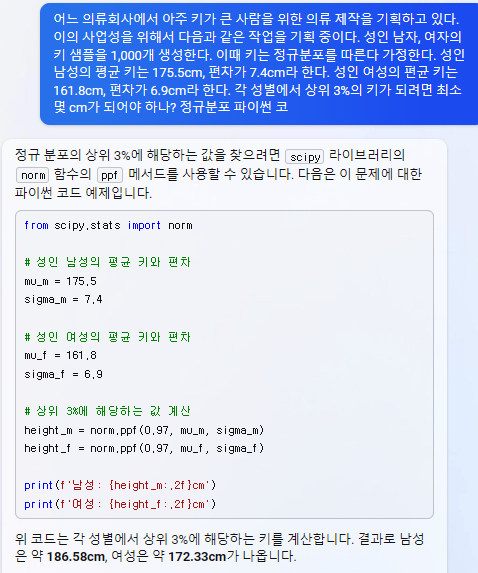
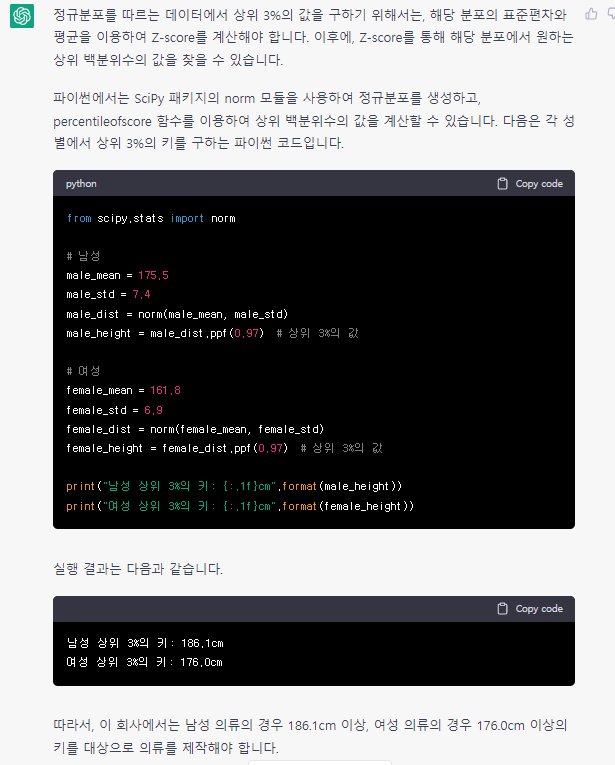
어느 의류회사에서 아주 키가 큰 사람을 위한 의류 제작을 기획하고 있다. 이의 사업성을 위해서 다음과 같은 작업을 기획 중이다.
성인 남자, 여자의 키 샘플을 1,000개 생성한다. 이때 키는 정규분포를 따른다 가정한다.
성인 남성의 평균 키는 175.5cm, 편차가 7.4cm라 한다.
성인 여성의 편균 키는 161.8cm, 편차가 6.9cm라 한다.
각 성별에서 상위 3%의 키가 되려면 최소 몇 cm가 되어야 하나?
from scipy.stats import norm
# 성인 남성의 평균 키와 편차
mu_m = 175.5
sigma_m = 7.4
# 성인 여성의 평균 키와 편차
mu_f = 161.8
sigma_f = 6.9
# 상위 3%에 해당하는 값 계산
height_m = norm.ppf(0.97, mu_m, sigma_m)
height_f = norm.ppf(0.97, mu_f, sigma_f)
print(f'남성: {height_m:.2f}cm')
print(f'여성: {height_f:.2f}cm')
답변) 위 코드는 각 성별에서 상위 3%에 해당하는 키를 계산합니다. 결과로 남성은 약 186.58cm, 여성은 약 172.33cm가 나옵니다.
'IT > 오랫만코딩:파이썬' 카테고리의 다른 글
| DAY14 로지스틱 회귀분석 및 군집분석-(Bing 챗(chat) GPT 생성한 파이썬 코드 첨삭) (0) | 2023.03.23 |
|---|---|
| DAY12 특징선택-feature selection 및 재현율 (recall)-(Bing 챗(chat) GPT 생성한 파이썬 코드 첨삭) (1) | 2023.03.21 |
| DAY 09 머신러닝 관련 Bing 챗(chat) GPT 생성한 파이썬 코드 및 동일 절차 Weka 실행 (0) | 2023.03.16 |
| DAY07 통계검정 (with OpenAI/Bing 챗(chat) GPT 생성한 파이썬 코드 첨삭) (0) | 2023.03.14 |
댓글